[LTSF] Are Transformers Effective for Time Series Forecasting?

 

Abstract

Transformer에서 위치 인코딩을 사용하고 서브시리즈를 임베딩하는 것은 일부 순서 정보를 유지하는 데 도움을 주지만, 변환 불변의 Self-attention machanism의 특성상 시간 정보 손실이 불가피합니다.

이 주장을 검증하기 위해, 비교를 위해 LTSF-Linear라는 매우 간단한 단일층 선형 모델 세트를 소개합니다. 9개의 실제 데이터셋에서 실험한 결과, LTSF-Linear는 기존의 복잡한 Transformer 기반 LTSF 모델들보다 모든 경우에서 놀랍게도 더 우수한 성능을 보였고 더불어, LTSF 모델의 다양한 설계 요소들이 시간적 관계 추출 능력에 미치는 영향을 탐구하는 포괄적인 경험적 연구를 수행했습니다. 향후 시계열 분석 작업(e.g., 이상 감지)을 위한 Transformer 기반 솔루션의 타당성을 재검토할 것을 권장합니다.

• 일단 제목부터 흥미가 돋는 문구에다가 당연히 최고의 성능일 것이라고 생각한 transformer architecture에 의문을 갖고 논문을 작성한 것이 굉장히 의미가 깊다.
• 물론 이러한 논문이 있다고 해서 transformer의 아성을 무너뜨릴 순 없다. 다만 경각심을 갖게 해주고 Task에 걸맞는 모델을 작성해야 한다는 것이 이 논문의 진짜 의도가 아닐까 감히 예상해본다.

1. Introduction

대표적인 모델로는 LogTrans [16] (NeurIPS 2019), Informer [30] (AAAI 2021 최우수 논문), Autoformer [28] (NeurIPS 2021), Pyraformer [18] (ICLR 2022 오럴), Triformer [5] (IJCAI 2022), 최근의 FEDformer [31] (ICML 2022) 등이 있습니다.

Transformer의 주요 작동 원리는 다중 헤드 자기 주의 메커니즘으로, 긴 시퀀스의 요소들 간의 의미적 상관관계를 추출하는 데 놀라운 능력을 가지고 있습니다. 그러나 자기 주의 메커니즘은 순열 불변성과 어느 정도의 "반순서성"을 가지고 있습니다. 다양한 유형의 위치 인코딩 기법을 사용하면 일부 순서 정보를 보존할 수 있지만, 자기 주의 메커니즘을 적용한 후에는 시간 정보 손실이 불가피합니다. 이는 의미가 풍부한 NLP와 같은 응용 분야에서는 큰 문제가 되지 않습니다. 예를 들어, 문장의 단어 순서를 재배열해도 문장의 의미는 크게 유지됩니다. 그러나 시계열 데이터를 분석할 때는 숫자 데이터 자체에 의미가 부족하며, 우리는 주로 연속적인 시점들 간의 시간적 변화를 모델링하는 데 관심이 있습니다. 즉, 순서 자체가 가장 중요한 역할을 합니다. 따라서 우리는 다음과 같은 흥미로운 질문을 제기합니다: Transformer가 정말로 장기 시계열 예측에 효과적인가?

• 위의 나오는 transformer의 이전 논문들은 제 블로그 포스팅에 작성되어 있으니 관심이 있다면 한번 보시는 것을 추천드립니다.

게다가, 기존의 Transformer 기반 LTSF 솔루션은 전통적인 방법에 비해 상당한 예측 정확도 향상을 보여주었지만, 실험에서 비교된 모든 (Transformer가 아닌) 기준선은 자가 회귀 또는 반복된 다중 스텝(IMS) 예측 [1,2,22,24]을 수행합니다. 이는 LTSF 문제에 대해 큰 오류 축적 효과를 겪는 것으로 알려져 있습니다. 따라서, 이 연구에서는 Transformer 기반 LTSF 솔루션을 직접 다중 스텝(DMS) 예측 전략으로 도전하여 실제 성능을 검증합니다.

요약하자면, 이 연구의 기여는 다음과 같습니다:

• 우리의 지식에 따르면, 이는 장기 시계열 예측 작업에 대한 Transformer의 유효성에 도전하는 첫 번째 연구입니다.
• 우리의 주장을 검증하기 위해, 기존의 Transformer 기반 LTSF 솔루션과 비교하기 위해 LTSF-Linear라는 매우 간단한 단일층 선형 모델 세트를 도입합니다. LTSF-Linear는 LTSF 문제에 대한 새로운 기준선이 될 수 있습니다.
• 기존 Transformer 기반 솔루션의 다양한 측면, 긴 입력을 모델링하는 능력, 시계열 순서에 대한 민감도, 위치 인코딩 및 서브시리즈 임베딩의 영향, 효율성 비교 등에 대한 포괄적인 경험적 연구를 수행합니다. 우리의 발견은 이 분야의 미래 연구에 도움이 될 것입니다.

• 이 논문이 LTSF라는 task의 하나의 축을 잡고 있는 논문이지만 이 뒤의 내용도 분명히 알아둬야할 이유들이 있습니다.
• 특히 임베딩, FFT, WL 등의 다양한 기법들이 시도되었고 각 논문들이 의미하는 바가 생각보다 크기에 이 Task에 대해서 깊게 공부하고 싶다면 가볍게 이전의 내용을 보고 오는 것을 추천드립니다.
  • 다만 모든 논문을 읽는 것은 쉽지 않기에 몇개 뽑아 보자면, LogTrans, Informer, Autoformer, FEDformer를 추천드리며 이 중에서 Autoformer과 FEDformer는 구조가 매우 유사하기 때문에 약 3개의 논문을 보고 오는 것을 추천드립니다. 

2. Preliminaries : TSF Problem Formulation

C개의 변수를 포함한 시계열 데이터 X={X1t,...,XCt}t=1LX = \{X^t_1, ..., X^t_C\}_{t=1}^LX={X1t​,...,XCt​}t=1L​ 에서 LLL은 조회 창의 크기이고, XitX^t_iXit​는 t 시점에서 i번째 변수의 값입니다. 시계열 예측 과제는 TTT 미래 시점에서 값 X^={X^1t,...,X^Ct}t=L+1L+T\hat{X} = \{\hat{X}^t_1, ..., \hat{X}^t_C\}_{t=L+1}^{L+T}X^={X^1t​,...,X^Ct​}t=L+1L+T​을 예측하는 것입니다.

3. Transformer 기반 LTSF 솔루션

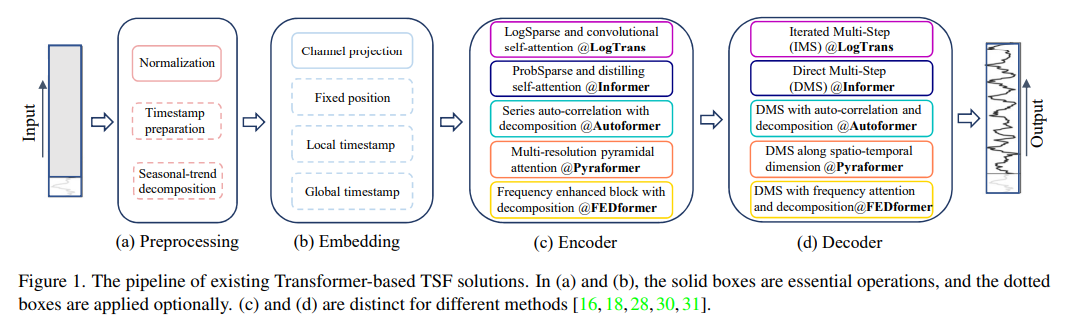
기본 Transformer 모델을 LTSF 문제에 적용할 때 몇 가지 한계가 있습니다. 첫째, 원래 Self attetion machanism의 시간/메모리 복잡도는 O(L^2)입니다. 둘째, Auto regression decoder 디자인은 오류 축적 문제를 야기합니다. Informer[30]는 이러한 문제를 해결하기 위해 새로운 Transformer 아키텍처와 DMS 예측 전략을 제안합니다. 

Time series decomposition

데이터 전처리를 위해, 정상화가 TSF에서 일반적입니다. Autoformer[28]는 각 신경 블록 뒤에 Season-Trend 분해를 적용합니다. 이는 시계열 분석에서 데이터를 더 예측 가능하게 만듭니다[6, 13]. 입력 시퀀스에 이동 평균 커널을 적용하여 추세-주기 성분을 추출합니다. 원래 시퀀스와 추세 성분의 차이는 계절 성분으로 간주됩니다. Autoformer의 분해 방식을 기반으로 FEDformer[31]는 다양한 커널 크기를 가진 이동 평균 커널로 추출한 추세 성분을 혼합하는 전략을 제안합니다.

• Autoformer에서 나온 TSF의 방식을 간략하게 설명하면 Trends는 smoothing 기법과 유사하며 특정 윈도우의 평균을 내는 방법입니다. 원본 값에서 Trends를 빼면 Season 데이터를 얻을 수 있습니다.
• FEDformer에서는 Autoformer에서 정해진 윈도우를 사용했다면 여기서는 가변 위도우를 이용해 가장 알맞는 윈도우를 찾는 방법을 이용합니다. 

Input embedding stragies

Transformer 아키텍처의 자기 주의 층은 시계열의 위치 정보를 보존할 수 없습니다. 그러나 시계열의 순서 정보는 중요합니다. 또한, 주간, 월간, 연간과 같은 계층적 타임스탬프 및 공휴일과 이벤트와 같은 시간 정보를 제공하는 것도 중요합니다

• 여기서는 위에서 말한 계층적 타임스탬프를 일반적인 positional embedding에 추가했다는 의미이며, convolution을 이용한 방법으로 주변 로컬 값을 가져오는 방법도 사용되었습니다.

Self attention machanism

Transformers는 Self attetnion machanism을 통해 쌍 요소 간의 의미적 의존성을 추출합니다. 최근 연구들은 기본 Transformer의 O(L^2)시간 및 메모리 복잡도를 줄이기 위해 두 가지 전략을 제안합니다. 한편으로는 LogTrans와 Pyraformer가 자기 주의 메커니즘에 희소성을 도입합니다. LogTrans는 로그희소 마스크를 사용하여 계산 복잡도를 O(L \log L)로 줄이고, Pyraformer는 피라미드 주의를 채택하여 계층적으로 다중 스케일 시간 의존성을 포착하여 O(L) 시간 및 메모리 복잡도를 달성합니다. 다른 한편으로는, Informer와 FEDformer가 자기 주의 행렬의 저차원 특성을 사용합니다. Informer는 확률희소 자기 주의 메커니즘과 자기 주의 증류 작업을 제안하여 복잡도를 O(L \log L)로 줄이며, FEDformer는 무작위 선택을 통해 Fourier 강화 블록과 웨이블릿 강화 블록을 설계하여 O(L) 복잡도를 달성합니다. 마지막으로, Autoformer는 원래 자기 주의 층을 시리즈 별 자기 상관 메커니즘으로 대체합니다.

• 간략하게 설명하자면 Self attention을 진행할 때, vanilla attention(다른 곳에서는 full-attention이라는 말로 사용합니다.)는 시퀀스 안의 모든 값과의 score를 구하는데, log, pyra등은 그 중에서 몇 개의 값만을 활용한다는 것입니다.
• 그 외로는 self attention을 직접 구하지 않고 FFT를 이용해서 구하기도 하는데, 이에 대한 자세한 내용은 관련 논문을 참조하시면 좀 더 도움이 될 것 같습니다.

Decoder

Transformer 모델의 전제는 쌍 요소 간의 의미적 상관관계이지만, 자기 주의 메커니즘 자체는 순열 불변입니다. 시계열 데이터의 원시 숫자 데이터(예: 주식 가격 또는 전기 값)에서는 포인트 간 의미적 상관관계가 거의 없습니다. 시계열 모델링에서는 연속적인 시점들 간의 시간적 관계에 주로 관심이 있으며, 이러한 요소들의 순서가 가장 중요한 역할을 합니다. 위치 인코딩과 서브시리즈 임베딩을 사용하는 것은 일부 순서 정보를 보존하는 데 도움이 되지만, 변환 불변의 자기 주의 메커니즘의 특성상 시간 정보 손실이 불가피합니다. 이러한 관찰을 바탕으로, 우리는 Transformer 기반 LTSF 솔루션의 유효성을 재검토하는 데 관심이 있습니다.

• 여기서도 이전의 논문들에서 사용된 Decoder들을 언급하는데, 참고해보시면 좋을 것 같습니다.
• 이 다음 내용을 설명하기 위해 DMS, IMS를 먼저 설명하겠습니다.
  • 반복적 다중 단계 예측 (IMS) 직접 다중 단계 예측 (DMS)
  • DMS 예측[4]은 한 번에 다중 단계 예측 목표를 최적화합니다. DMS 예측은 단일 단계 예측 모델을 학습하는 대신, 여러 미래 시점을 한꺼번에 예측합니다. 이 방법은 단일 단계 예측 모델을 얻기 어렵거나 T가 클 때 더 정확한 예측을 생성할 수 있습니다. DMS 예측은 여러 시점의 값을 한 번에 예측하기 때문에, 긴 시계열 예측 문제에서 오류 축적 문제를 피할 수 있습니다.
  • IMS 예측[23]은 단일 단계 예측기를 학습하고 이를 반복적으로 적용하여 다중 단계 예측을 얻습니다. 이는 예측된 값을 다시 입력으로 사용하여 다음 시점의 값을 예측하는 방식입니다. 이 방법은 자기 회귀(estimation procedure) 과정 덕분에 작은 분산을 가지지만, 오류 축적 효과가 불가피합니다. 따라서 IMS 예측은 매우 정확한 단일 단계 예측기가 있을 때 선호되며, T가 상대적으로 작을 때 유리합니다.

• 제가 이해했을 때, 이 논문은 결국 기존의 transformer 변형 모델들이 성능이 향상된 이유는 IMS의 방식이 아닌 DMS를 했기 때문이라고 이해했습니다. 따라서 실제로 transformer의 논문 향상은 transformer 덕분이 아닌 그저 DMS를 사용했기 때문이다라는 것입니다.
• 그렇기에 저자들은 transformer를 쓰지 않고 DMS를 했을 때, 꽤 잘 나온다면 transformer가 성능에 기여한 바는 크지 않다는 것을 보여준 것입니다.

4. An Embarrassingly Simple Baseline

기존 Transformer 기반 LTSF 솔루션(T \gg 1)의 실험에서는 비교된 모든 (Transformer가 아닌) 기준선이 IMS 예측 기술로 알려져 있으며, 이는 LTSF 문제에서 심각한 오류 축적 효과를 겪는 것으로 알려져 있습니다. 이러한 연구들의 성능 향상이 주로 DMS 전략 덕분이라고 가정합니다.

4.1 LTSF-Linear

이 가설을 검증하기 위해, 기본 DMS 모델을 시간적 선형 층을 통해 제시하며, 이를 기준선으로 사용합니다. 기본 LTSF-Linear 모델은 역사적 시계열 데이터를 기반으로 미래 시계열을 예측하기 위해 가중합 연산을 사용하는 것으로 설명할 수 있습니다(그림 2 참조). 수학적 표현은 X^i=WXi\hat{X}^i = W X^iX^i=WXi이며, 여기서 W∈RT×LW \in \mathbb{R}^{T \times L}W∈RT×L은 시간 축을 따라 선형 층입니다. X^i\hat{X}^iX^i와 XiX^iXi는 각 i번째 변수의 예측과 입력을 나타냅니다. LTSF-Linear는 다른 변수들 간의 공간적 상관관계를 모델링하지 않으며, 가중치를 공유합니다.

LTSF-Linear는 여러 선형 모델 세트입니다. Vanilla Linear는 단일 층 선형 모델입니다. 금융, 교통, 에너지 도메인 등 다양한 도메인에서 시계열을 처리하기 위해 두 가지 전처리 방법을 가진 두 가지 변형을 추가로 도입합니다: DLinear와 NLinear입니다.

1. DLinear: Autoformer 및 FEDformer에서 사용된 분해 방식과 선형 층의 조합입니다. 먼저 이동 평균 커널을 통해 입력 데이터를 추세 성분과 나머지(계절 성분) 성분으로 분해합니다. 그런 다음, 각 성분에 두 개의 단일 층 선형 층을 적용하고, 두 특징을 합산하여 최종 예측을 얻습니다. DLinear는 데이터에 명확한 추세가 있을 때 Vanilla Linear보다 성능이 향상됩니다.
2. NLinear: 데이터셋에서 분포 변화가 있을 때 LTSF-Linear의 성능을 향상시키기 위해, NLinear는 먼저 시퀀스의 마지막 값을 기준으로 입력을 뺍니다. 그런 다음 입력은 선형 층을 통과하며, 뺀 부분을 다시 추가하여 최종 예측을 만듭니다. NLinear의 뺄셈과 덧셈은 입력 시퀀스에 대한 간단한 정규화입니다.

5. Experiments

5.1 Experiments Settings

데이터셋: 우리는 9개의 널리 사용되는 실제 데이터셋에서 광범위한 실험을 수행합니다. 여기에는 ETT (전기 변압기 온도) [30] (ETTh1, ETTh2, ETTm1, ETTm2), Traffic, Electricity, Weather, ILI, Exchange-Rate [15]가 포함됩니다. 모든 데이터셋은 다변량 시계열입니다. 데이터 설명은 부록에 나와 있습니다.

평가 지표: 이전 연구 [28, 30, 31]를 따라, 우리는 MSE (평균 제곱 오차)와 MAE (평균 절대 오차)를 핵심 지표로 사용하여 성능을 비교합니다.

비교 방법: 우리는 최근의 Transformer 기반 방법인 FEDformer [31], Autoformer [28], Informer [30], Pyraformer [18], LogTrans [16]를 포함합니다. 또한 가장 간단한 DMS 방법인 Closest Repeat (Repeat)도 포함하여 마지막 값을 반복하는 기준선으로 사용합니다. FEDformer의 두 가지 변형 중 더 나은 정확도를 보이는 FEDformer-f를 비교합니다.

5.2 Comparision with Transformers

정량적 결과: 표 2에서, 우리는 언급된 모든 Transformer 모델을 9개의 벤치마크에서 광범위하게 평가합니다. 놀랍게도, LTSF-Linear의 성능이 대부분의 경우 SOTA FEDformer를 20% ~ 50% 향상시키는 것을 확인할 수 있었습니다. 이는 LTSF-Linear가 변수들 간의 상관관계를 모델링하지 않음에도 불구하고 다변량 예측에서 더 나은 성능을 보임을 의미합니다. 다양한 시계열 벤치마크에서 NLinear와 DLinear는 분포 변화와 추세-계절성 특징을 처리하는 데 우월함을 보여줍니다. 또한, 우리는 부록에 ETT 데이터셋의 단변량 예측 결과를 제공하며, 여기서도 LTSF-Linear가 Transformer 기반 LTSF 솔루션을 큰 차이로 능가함을 확인할 수 있습니다.

정성적 결과: 그림 3에서, 우리는 Electricity (시퀀스 1951, 변수 36), Exchange-Rate (시퀀스 676, 변수 3), ETTh2 (시퀀스 1241, 변수 2) 데이터셋에서 Transformer 기반 솔루션과 LTSF-Linear의 예측 결과를 시각화했습니다. 입력 길이가 96 스텝이고 출력 지평이 336 스텝일 때, Transformer [28, 30, 31]는 미래 데이터의 스케일과 바이어스를 포착하지 못했습니다. 또한, Exchange-Rate와 같은 비주기적 데이터에서는 적절한 추세를 예측하지 못했습니다. 이러한 현상은 기존 Transformer 기반 솔루션이 LTSF 작업에서 적절하지 않음을 추가로 나타냅니다.

5.3 LTSF-Transformers에 대한 추가 분석

기존 LTSF-Transformers가 긴 입력 시퀀스에서 시간적 관계를 잘 추출할 수 있는가? 입력 조회 창의 크기는 예측 정확도에 큰 영향을 미칩니다. 일반적으로, 강력한 TSF 모델은 강력한 시간적 관계 추출 능력을 가지고 있어야 하며, 더 큰 조회 창 크기에서 더 나은 결과를 달성할 수 있어야 합니다. 입력 조회 창 크기 L을 {24, 48, 72, 96, 120, 144, 168, 192, 336, 504, 672, 720}로 설정하여 장기 예측(T=720)을 수행한 결과, 기존 Transformer 기반 모델의 성능은 조회 창 크기가 증가할 때 악화되거나 유지되었지만, 모든 LTSF-Linear 모델의 성능은 조회 창 크기가 증가할 때 크게 향상되었습니다.

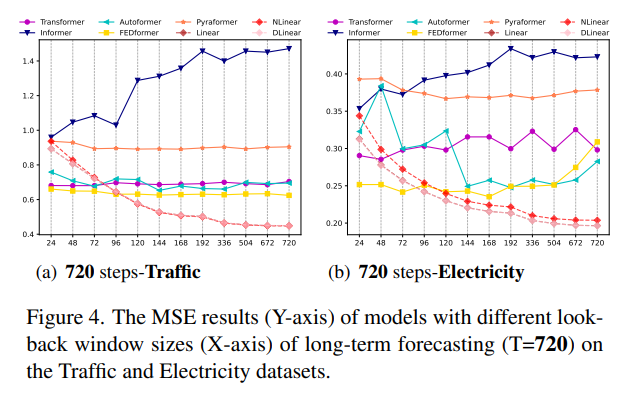
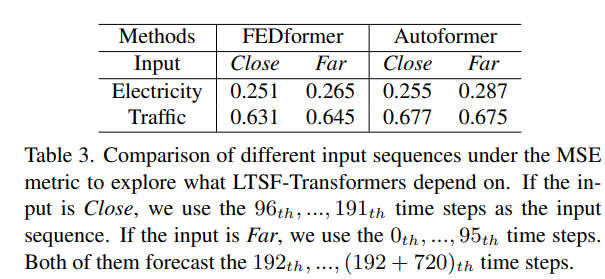
장기 예측에서 무엇을 배울 수 있는가? 조회 창 내의 시간적 동적 변화는 단기 시계열 예측 정확도에 큰 영향을 미치지만, 장기 예측은 모델이 추세와 주기성을 잘 포착할 수 있는지에 달려 있습니다. 예측 지평이 멀어질수록 조회 창 자체의 영향은 감소합니다. 실험 결과, SOTA Transformers의 성능은 근접 조회 창보다 먼 조회 창을 사용할 때 약간 떨어졌습니다. 이는 이러한 모델이 인접한 시계열 시퀀스에서 유사한 시간적 정보를 캡처하는 데만 의존한다는 것을 나타냅니다.

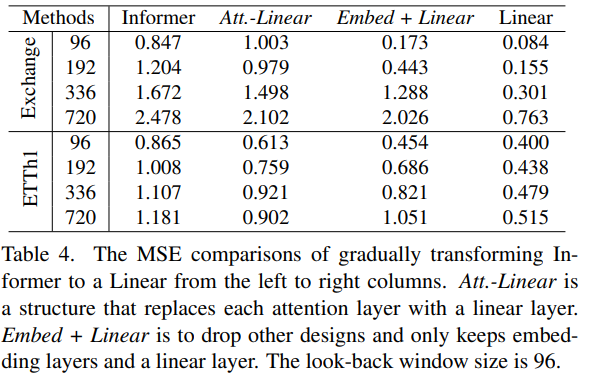
자기 주의 메커니즘이 LTSF에 효과적인가? 기존 Transformer (e.g., Informer)의 복잡한 설계가 필수적인지 여부를 확인했습니다. 각 자기 주의 층을 선형 층으로 대체한 결과, 성능이 점진적으로 향상되었습니다. 이는 최소한 기존 LTSF 벤치마크에서는 자기 주의 메커니즘과 다른 복잡한 모듈이 불필요함을 나타냅니다.

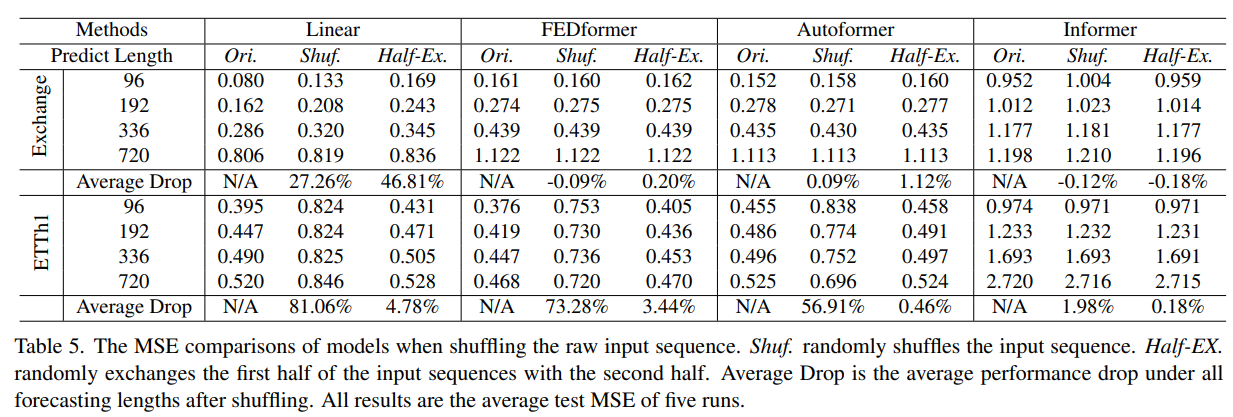
기존 LTSF-Transformers가 시간 순서를 잘 보존할 수 있는가? 자기 주의 메커니즘은 본질적으로 순열 불변이므로, 시퀀스 순서가 중요한 시계열 예측에서 문제가 될 수 있습니다. 입력 시퀀스를 무작위로 섞거나 반으로 나누어 교환한 후 실험한 결과, 대부분의 Transformer 기반 모델의 성능은 크게 변하지 않았지만, LTSF-Linear 모델의 성능은 크게 저하되었습니다. 이는 Transformer 기반 모델이 시간 순서를 잘 보존하지 못하며, 잡음에 과적합되기 쉽다는 것을 의미합니다.

다양한 임베딩 전략의 효과는? 위치와 타임스탬프 임베딩이 Transformer 기반 모델에 미치는 영향을 연구했습니다. Informer는 각 토큰에 단일 타임스탬프를 사용하기 때문에, 타임스탬프 임베딩이 없을 때 성능이 크게 감소했습니다. FEDformer와 Autoformer는 시퀀스의 타임스탬프를 사용하여 시간 정보를 임베딩하기 때문에, 고정 위치 인코딩 없이도 더 나은 성능을 달성할 수 있습니다. 그러나 타임스탬프 임베딩이 없으면 Autoformer의 성능은 급격히 감소합니다. 이는 FEDformer가 제안된 주파수 강화 모듈 덕분에 시간적 유도 편향을 도입하여, 어떤 위치/타임스탬프 임베딩이 없더라도 성능 저하가 적다는 것을 의미합니다.

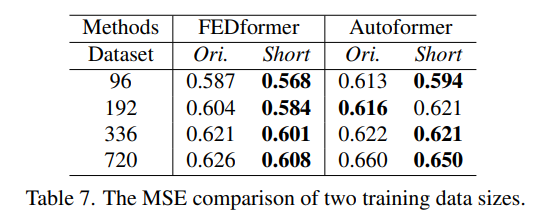
훈련 데이터 크기가 기존 LTSF-Transformers의 제한 요소인가? Transformer 기반 솔루션의 성능 저하가 데이터셋 크기 때문이라는 주장도 있을 수 있습니다. 훈련 데이터 크기가 모델 성능에 미치는 영향을 조사하기 위해 Traffic 데이터셋에서 전체 데이터셋과 축소된 데이터셋(1년 데이터)으로 모델을 훈련한 결과, 축소된 데이터셋으로 훈련했을 때 예측 오류가 오히려 낮아지는 경우가 많았습니다. 이는 전체 연도 데이터가 더 명확한 시간적 특징을 유지하기 때문일 수 있습니다. 따라서 훈련 데이터 크기는 Autoformer와 FEDformer의 성능 저하의 제한 요소가 아님을 나타냅니다.

효율성이 정말 중요한가? 기존 LTSF-Transformers는 O(L^2)복잡도가 LTSF 문제에 부담이 된다고 주장합니다. 실험 결과, 대부분의 Transformer 변형은 유사하거나 더 높은 실제 추론 시간과 메모리 사용량을 보였습니다. 이는 적어도 기존 벤치마크에서는 메모리 효율성이 큰 문제가 아님을 나타냅니다.

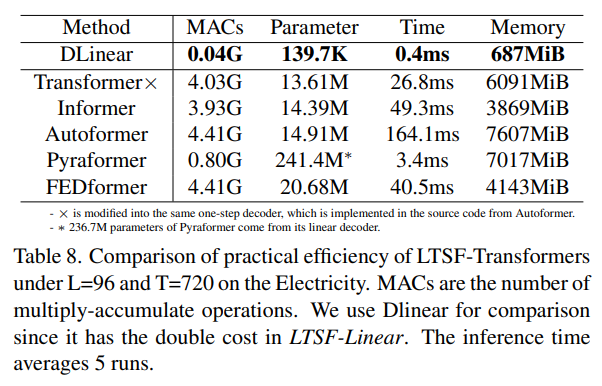
• 저는 이 추가 연구가 아마 revision때 받은 질문들을 정리해놓은 것이라고 생각했는데, 그렇다면 여기에서 이 효율성에 관한 질문이 왜 나왔는지 이해하기가 어려웠습니다. 이 문단의 요약은 결국 '요즘 좋은 메모리가 큰 GPU가 많은데 우리가 굳이 메모리 효율성을 챙기기 위해서 성능을 줄이는 게 맞는 가?' 에 대한 질문인데, 저자들은 최소한 지금에서는 그럴 필요가 없다는 것으로 말하고 있습니다.
• 제가 이해하기로는 이 논문 이후로 transformer의 메모리 복잡성에 얽매이지말고 시간, 공간 복잡도가 다소 높더라도 선형 모델 정도는 이길만한 성능이 나와야한다고 마치 장려하는 것과 같은 메세지를 던진 것 같습니다.

6. 결론 및 향후 연구

결론: 본 연구는 장기 시계열 예측 문제에 대한 Transformer 기반 솔루션의 유효성에 의문을 제기합니다. 매우 간단한 선형 모델인 LTSF-Linear를 사용하여 우리의 주장을 검증하였습니다. 우리의 기여는 선형 모델을 제안하는 것보다는 중요한 질문을 던지고, 놀라운 비교 결과를 보여주며, 다양한 관점에서 Transformer 기반 LTSF 모델이 왜 효과적이지 않은지 설명하는 데 있습니다. 우리는 이 연구가 이 분야의 미래 연구에 도움이 되기를 바랍니다.

향후 연구: LTSF-Linear는 제한된 모델 용량을 가지며, 단순하지만 경쟁력 있는 기준선으로서 향후 연구를 위한 강력한 해석 가능성을 제공합니다. 예를 들어, 단층 선형 네트워크는 변화 지점에 의해 발생하는 시간 역학을 포착하기 어렵습니다. 따라서 새로운 모델 설계, 데이터 처리 및 벤치마크에 큰 잠재력이 있다고 생각합니다.

• 결론에서 주의 깊게 봐야할 점은 Transformer의 변형 모델들이 전부 쓸모 없었다라는 것이 아님을 강조하고 있었습니다. 다만 저자들은 하나의 기준점을 제시했을 뿐이고, 이를 통해서 더 좋은 모델을 만들어내는 계기가 되었다는 것을 알아두면 좋을 것 같습니다.

---

코드분석

 

 

---

참고자료

1. https://arxiv.org/abs/2205.13504

Are Transformers Effective for Time Series Forecasting?

2. https://github.com/cure-lab/LTSF-Linear

GitHub - cure-lab/LTSF-Linear: [AAAI-23 Oral] Official implementation of the paper "Are Transformers Effective for Time Series F